选择算法：在列表或数组中找到第k个最小的数字的算法。

这样的数字被称为第k个顺序统计量(order statistic)

最简单粗暴的方法即对数据排序，得到 \(O(nlogn)\) 复杂度的算法。

但毫无疑问，整体排序做了不少多余的工作。下面介绍两重基于快排的算法，能够在 \(o(n)\) 时间内找到top k元素。

快排划分

考虑在快排中，子集的划分：选取一个主元(pivot)，任意比主元小的元素都在主元左边，任意比主元大的元素都在主元右边。

这便是一个天然的top k元素。虽然不具备”直达性”，但是能够通过递归最终得到需要的top k元素。

快排中的划分函数partition如下：

// p means the start of the array while r means the end of the array
int partition(int *array, int p, int r) {
    int pivot = array[r];
    int pivotPosition = 0;
    for (int i = 0; i < r - p + 1; i++) {
        if (array[i] < pivot) {
            swap(array, i, pivotPosition);
            pivotPosition++;
        }
    }
    swap(array, r, pivotPosition);
    return pivotPosition;
}

其中swap为交换两元素位置

partition的复杂度为 \(O(n)\)

考虑到每次划分选取array[r]作为主元并不”快”，复杂度与输入强相关。因此引入随机量，将其转换为一个随机化算法。即每次随机地从array中取得一个元素作为主元。从而得到较好的期望。

改进为randomizePartition如下：

int randomizePartition(int *array, int p, int r) {
    srand(time(NULL));
    int x = rand() % (r - p + 1) + p;
    swap(array, x, r);
    return partition(array, p, r);
}

此时复杂度仍然为 \(O(n)\)。但是拥有了更好的期望，且很难出现最坏的输入排列。

证明如下:

\[\mbox{assume we want to find the maximum number. And the partition is the increasing order}\\ \mbox{Let }A_{n} \mbox{be the event: the pivot is the minimum one in the array of length n, then}\\ P(A_{n}) = \frac{1}{n} \\ \mbox{Let T be the event: the worst case -- decreasing one number once, then}\\ T = \prod_{i=0}^{n}A_{i} \\ \mbox{because }A_{i} \mbox{ and } A_{j} \mbox{ are independent, then}\\ P(T) = P(\prod_{i=0}^{n}A_{i}) = \prod_{i=0}^{n} P(A_{i}) = \prod_{i=1}^{n} \frac{1}{i} = \frac{1}{n!}\]

因此，当n很大时，发生最坏情况的概率趋近于0

QuickSelect

基于快排中partition的简单改进。

注意到在快排中，每次选取主元后，同时在左右两边进行递归。但是在Top k问题中，仅需要在一边进行递归即可。

通过判断每次选取的主元为Top几，从而判断在左边还是右边进行递归。从而降低了复杂度。

同时，又由于采用randomizePartition，此时的quickSelect为一随机化算法。拥有较好的期望值。

randomizeSelect如下：

// array[i] means the i-th largest element
int randomizeSelect(int *array, int p, int r, int i) {
    if (p == r) return array[r];

    // k means the position of pivot in the array
    int k = randomizePartition(array, p, r);
    // nthMin means pivot is the n-th minimum of the array[p..r]
    int nthMin = k - p + 1;
    if (nthMin == i) {
        return array[k];
    }

    if (nthMin > i) {
        return randomizeSelect(array, p, k - 1, i);
    } else {
        return randomizeSelect(array, k + 1, r, i - nthMin);
    }
}

其时间复杂度的期望为 \(O(n)\)。但是最坏情况下为 \(O(n^2)\)。

BFPTR

一种复杂度十分优秀的算法。最坏情况下依旧为 \(O(n)\) 复杂度的选择算法。是对QuickSelect算法的一种优化。

注意到哪怕采用了randomizeSelect，依旧难以从根本上避免最坏的情况：每次划分仅减少1个数。

随机化只是从概率上使得上述最坏情况较难发生而已。而BTPTR算法是从本质上降低了时间复杂度。

叫BFPTR是因为该算法首次由Blum、Floyd、Pratt、Rivest、Tarjan发布于Blum et al. (1973)。

在原paper中，称之为 “PICK”。而将quickSelect称之为 “FIND”

BFPTR算法的改进之处在于通过在线性时间内选取一个特殊的主元(pivot)，从而在每次执行partition时总能得到好的划分。

主元选取做法如下：

将数组中的n个元素划分为 \(\lfloor \frac{n}{5} \rfloor\) 组，即每组5个数（最后一组为5个或小于5个）
对每组执行插入排序（或者其他排序），而后得到每组的中位数（若偶数个元素，则取靠近左边界的那个）
对上述步骤选出的 \(\lceil \frac{n}{5} \rceil\) 个中位数, 选出他们的中位数 \(x\)

\(x\) 即为所需主元

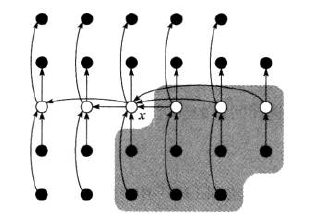
median-of-median

如上图所示，对于 主元(pivot) \(x\), 其左上角的元素总是小于它的，右下角的元素总是大于它的。从而每次划分至少能够减少30%的规模，从而使得每次递归规模对数级下降。

在实现中，上述步骤有两个细节应该注意：

每次执行插入排序后将选取出的中位数集中，便于继续得到他们的中位数。

需要的仅仅是他们的中位数，而不是将其排序。有序过程由partition生成。

得到中位数的中位数过程中存在一个互递归(mutual recursion)。

即使用解决Top k问题的函数BFPTRSelect去得到median of median

哪怕对每组实行插入排序，整体增加的时间复杂的也只是 \(n \times \lfloor \frac{n}{5} \rfloor = O(n)\)

具体代码实现如下：

以下返回值大多为数组下标Index

通过插入排序获取五个数中的中位数：

int medianSelect5Index(int *array, int start, int end) {
    if (start == end) {
        return start;
    }

    for (int i = start; i <= end; i++) {
        int minElement = array[i];
        int minIndex = i;
        for (int j = i; j <= end; j++) {
            if (array[j] < minElement) {
                minIndex = j;
                minElement = array[j];
            }
        }
        exchange(array, i, minIndex);
    }

    return (start + end) / 2;
}

获取主元——中位数的中位数(median of median), 注意其结尾return处与算法主体的一个互递归

nt getMedianOfMedianIndex(int *array, int start, int end) {
    if (end - start < 5) {
        return medianSelect5Index(array, start, end);
    }

    // get each median of 5 number and make them together in front of the array
    for (int i = start; i <= end; i += 5) {
        int subEnd = i + 4;
        if (subEnd > end) {
            subEnd = end;
        }

        int media = medianSelect5Index(array, start, subEnd);
        exchange(array, media, start + (i / 5));
    }

    // medianNum is the upper bound of the `(end - start + 1) / 5`
    int medianNum;
    if ((end - start + 1) % 5 == 0) {
        medianNum = (end - start + 1) / 5;
    } else {
        medianNum = (end - start + 1) / 5 + 1;
    }

    int medianEnd = start + medianNum - 1;

    // by mutual recursion, get the median index of the medians
    return BFPTRSelectIndex(array, start, medianEnd, medianNum / 2);
}

改进后的子集划分:

int BFPTRPartition(int *array, int start, int end) {
    int medianOfMedianIndex = getMedianOfMedianIndex(array, start, end);
    exchange(array, end, medianOfMedianIndex);
    return partition(array, start, end);
}

BFPTR算法主体：

int BFPTRSelectIndex(int *array, int start, int end, int k) {
    if (start == end) {
        return start;
    }

    int pivotIndex = BFPTRPartition(array, start, end);

    int nthMin = pivotIndex - start + 1;

    if (nthMin == k) {
        return pivotIndex;
    } else if (nthMin > k) {
        return BFPTRSelectIndex(array, start, pivotIndex - 1, k);
    } else {
        return BFPTRSelectIndex(array, pivotIndex + 1, end, k - nthMin);
    }
}

注意：上述BFPTRSelectIndex返回值为top k在数组中的位置。若要取值，应再封装一层

此即得到了一个最坏情况下复杂度仍为 \(O(n)\) 的算法。

附录

BFPTR算法时间复杂度的分析

对每次选取的主元 \(x\)，其为中位数的中位数。意味着在选取出的中位数中，至少有一半的数大于等于 \(x\),而在这 \(\lfloor \frac{n}{5} \rfloor\) 组中，除去最后一组的含有 \(x\) 的那组外，至少有一半的组(中位数大于x的那些组)有至少三个元素大于 \(x\) 。

因此，大于x的元素个数至少为： \(3 \cdot ( \lceil \frac{1}{2} \cdot \lceil \frac{n}{5} \rceil \rceil - 2) \ge \frac{3n}{10} - 6\)

同样地，至少有 \(\frac{3n}{10} - 6\) 个元素小于 \(x\)

因此，BFPTRSelect递归时，至多作用于 \(n - (\frac{3n}{10} - 6) = \frac{7n}{10} + 6\) 个元素

取 \(T(n)\) 为数组长度为n时算法的时间复杂度，从而得到如下递归关系式：

\[\begin{equation} T(n) = \left\{ \begin{array}{ll} O(1) & n \lt 140 \\ T(\frac{7n}{10} + 6) + T(\lceil \frac{n}{5} \rceil) + O(n) & n \ge 140 \end{array} \right. \end{equation}\]

其中, \(T(\lceil \frac{n}{5} \rceil) + O(n)\) . 为互递归获取median of median的代价

解得 \(T(n) = O(n)\)

Top K Question

快排划分

QuickSelect

BFPTR

通过插入排序获取五个数中的中位数：

附录

BFPTR算法时间复杂度的分析

Reference